Ежедневные тесты
Меню курса
Март
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. Уровень сложности "реального экзамена" примерно 0-40%. Более сложные задачи тоже из ФИПИ, но это редкость. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
В треугольнике \(ABC\) угол \(C\) равен 90°, \(CH\) - высота, \(BC = 15\), \(\cos{A} = \dfrac{\sqrt{35}}{6}\). Найдите \(AH\).
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите косинус угла между ними.

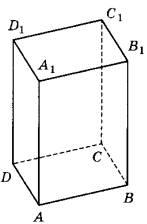
Дана правильная четырёхугольная призма ABCDA₁B₁C₁D₁, площадь основания которой равна 8, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки A, B, C, A₁, B₁.
Игральный кубик бросают два раза. Найдите вероятность того, что сумма выпавших очков будет больше 8. Результат округлите до сотых.
В торговом центре стоят три платежных терминала. Каждый из них может быть неисправен с вероятностью 0,1 независимо от других. Найдите вероятность того, что ровно один терминал неисправен.
Решите уравнение \(\dfrac5{x^3-2x^2-2x+1}-\dfrac{2}{x^3-4x^2+4x-1}=\dfrac1{x^2-1}\). Если корней несколько, в ответ запишите больший из них.
Найдите значение выражения \(\dfrac{8^{2{,}8}\cdot 5^{3{,}2}}{20^{2{,}2}}\)
Прямая \(y=-6x-7\) является касательной к графику функции \(f(x)=4x^2-18x+c\). Найдите \(c\).
Независимое агентство намерено ввести рейтинг \(R\) новостных интернет-изданий на основе оценок информативности \(In\), оперативности \(Op\), объективности \(Tr\) публикаций, а также качества \(Q\) сайта. Каждый отдельный показатель - целое число от 0 до 4. Составители рейтинга считают, что объективность публикаций ценится вчетверо, а информативность - впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид \(R=\dfrac{5In+Op+4Tr+ Q}{A}.\) Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число \(A\), при котором это условие будет выполняться.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 16 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
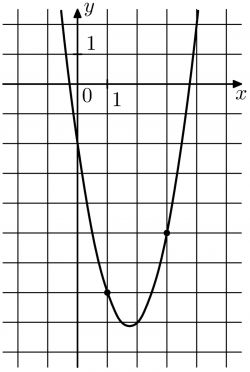
На рисунке изображен график функции вида \(f(x)=2x^2+bx+c\). Найдите \(f(-2)\).
Найдите точку максимума функции \(y=4+27x-2x\sqrt{x}\)
а) Решите уравнение \(750^{\cos3x}+6\cdot 125^{\frac13+\cos3x}=5^{5\cos3x}+30^{1+\cos3x}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}4;-\dfrac{3\pi}4\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. π/6+πn/3, n∈Z | 2. π/4+πn/3, n∈Z | 3. π/3+πn/6, n∈Z | 4. π/2+πn/4, n∈Z |
б)
| 5. -7π/4 | 6. -5π/3 | 7. -3π/2 | 8. -4π/3 |
| 9. -5π/4 | 10. -7π/6 | 11. -π | 12. -5π/6 |
В правильной призме ABCA₁B₁C₁ сторона AB основания ABC равна 4, а боковое ребро AA₁ равно 6. На рёбрах BB₁, CC₁ и A₁B₁ соответственно отмечены точки N, K и P так, что CK:KC₁=B₁N:NB=B₁P:PA₁=1:2. Плоскость KNP пересекает ребро A₁C₁ в точке F.
а) Докажите, что точка F — середина ребра A₁C₁.
б) Найдите расстояние от точки F до плоскости ANK.
Решите неравенство \((4^x-5\cdot 2^x)^2-20(4^x-5\cdot2^x)\leqslant96\)
15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
– 15-го числа 15-го месяца долг составит 100 тысяч рублей;
– к 15-му числу 16-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.
На стороне BC ромба ABCD отметили точку E так, что BE:EC=1:3. Через точку E перпендикулярно BC провели прямую, которая пересекает диагонали BD и AC в точках R и M соответственно, при этом BR:RD=1:2.
а) Докажите, что точка M делит отрезок AC в отношении 3:2, считая от вершины C.
б) Найдите периметр ромба ABCD, если MR=√15.
Найдите все значения \(a\), при каждом из которых уравнение \(\sqrt{3x+18-x^2}-2a=a|x|+1\) имеет ровно один корень.
На доске написано более 35, но менее 49 целых чисел. Среднее арифметическое этих чисел равно 5, среднее арифметическое всех положительных из них равно 14, а среднее арифметическое всех отрицательных из них равно -7.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше, положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Введите ответ в форме строки "11;п;1234". Где ответы на пункты разделены ";", и второй ответ "п", если положительных или "о", если отрицательных.