Ежедневные тесты
Меню курса
Февраль
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. Уровень сложности "реального экзамена" примерно 0-40%. Более сложные задачи тоже из ФИПИ, но это редкость. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
Окружность, вписанная в равнобедренный треугольник ABC, касается его боковых сторон в точках E и F. Найдите периметр треугольника ABC, если его основание равно AC=12, а отрезок EF=3.
Даны векторы \(\vec{a}(0;3)\), \(\vec{b}(-2;4)\) и \(\vec{c}(4;-1)\). Найдите длину вектора \(\vec{a}+2\vec{b}+\vec{c}\)
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Рубин» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Рубин» выиграет жребий ровно два раза.
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 4 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 7 мая в Волшебной стране будет отличная погода.
Решите уравнение \(4(\sqrt5-2)^{x-15}=\left(\dfrac2{\sqrt5+2}\right)^{x-15}\)
Найдите значение выражения \(\sqrt{8} - \sqrt{32}\sin^2 \dfrac{11\pi}{8}\)
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2, ..., x_9\). Сколько из этих точек принадлежат промежуткам убывания функции \(f(x)\)?

Водолазный колокол, содержащий \(\nu=5\) моль воздуха при объём \(V_1=26\,л\) , медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма \(V_2\) (в л). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log_2{\dfrac{V_1}{V_2}}\), где \(\alpha=8{,}5\, \dfrac{Дж}{моль\cdot К}\) – постоянная, \(T=300\, К\) – температура воздуха. Найдите, какой объём \(V_2\) будет занимать воздух в колоколе, если при сжатии воздуха была совершена работа в \(25500\, Дж\). Ответ дайте в литрах.
Юля и Оля пропалывают грядку за 5 минут, а одна Оля — за 30 минут. За сколько минут пропалывает грядку одна Юля?
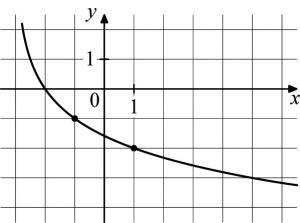
На рисунке изображен график функции \(f(x)=\log_a(x+b)\). Найдите \(f(-2{,}75)\).
Найдите точку максимума функции \(y=(x+8)^2\cdot e^{3-x}\)
а) Решите уравнение \(7\cos{x}-4\cos^3{x}=2\sqrt{3}\sin{2x}\).
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-4\pi;-3\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали трапеции пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD=8,5, BC=7,5, SO=6,5, а прямая SO перпендикулярна прямой AD.
Решите неравенство \(\dfrac{16^{x+0{,}5}-4^{x+1{,}5}-4}{4^x-2}+\dfrac{100}{4^x-8}\geqslant4^{x+1}-24\)
Производство \(x\) тыс. единиц продуктции обходится в \(q=2x^2+5x+10\) млн рублей в год. При цене \(p\) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет \(px-q\). При каком наименьшем значении \(p\) через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении \(x\)?
В треугольнике ABC точки N и P — середины сторон AB и BC соответственно. Отрезок NP касается окружности, вписанной в треугольник ABC.
а) Докажите, что периметр треугольника ABC равен 4AC.
б) Найдите площадь треугольника ABC, если его периметр равен 28, ∠BAC=120°.
Найдите все такие значения \(a\), при каждом из которых уравнение \(\sqrt{10x^2+x-24}\cdot\log_2((x-3)(a+5)+14)=0\) имеет ровно два различных корня.
Сторона квадрата на 3 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
а) Может ли ширина прямоугольника быть равной 8?
б) Может ли длина прямоугольника быть равной 16?
в) Найдите все возможные варианты таких пар прямоугольников и квадратов.
Введите ответ в форме строки "да;да;1;2;3;4". Где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а в пункте В перечислите возможные длины стороны квадрата по возрастанию через точку с запятой.