Тесты ОГЭ

Вычислите \(\dfrac{3}{4} - \dfrac{4}{5}\).

На координатной прямой отмечено число \(a\). Из представленных утверждений выберите верное.

​

1) \((a-6)^2>1\)
2) \((a-7)^2>1\)
3) \(a^2>36\)
4) \(a^2>49\)

Найдите значение выражения: \(\sqrt{\dfrac{16a^{12}}{a^{10}}}\), при \(a=5\)

Решите уравнение \((x+10)^2 = (5-x)^2\).

Саша, Семен, Зоя и Лера бросили жребий - кому начинать игру. Найдите вероятность того, что начинать игру должен будет не Семен.

Установите соответствие между функциями и их графиками.

ФУНКЦИИ:

А) \(y = -x^2 + 2x + 5\)

Б) \(y = x^2 + 2x + 5\)

В) \(y = -x^2 - 2x + 5\)

ГРАФИКИ:

​В ответ запишите цифры в порядке, соответствующем буквам АБВ.

В фирме "Чистая вода" стоимость (в рублях) колодца из железобетонных колец рассчитывается по фоомуле C=6500+4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец. Ответ укажите в рублях.

Выберите верное множество решений неравенства \(x^2-2x-3\geqslant 0\).

1) (-∞;-1)∪(3;+∞)
2) (-1;3)
3)(-∞;-1]∪[3;+∞)
4) [-1;3]

Геометрическая прогрессия \((b_{n})\) задана условиями: \(b_{1}= -1\), \(b_{n+1}=2b_{n}\). Найдите \(b_{7}\).

Точка \(D\) на стороне \(AB\) треугольника \(ABC\) выбрана так, что \(AD=AC\). Известно, что \(\angle{CAB}= 80^{\circ}\), \(\angle{ACB}= 59^{\circ}\). Найдите угол \(DCB\). Ответ дайте в градусах.

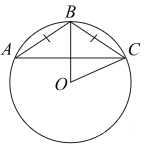
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

​

Найдите площадь трапеции, изображённой на рисунке.

Найдите тангенс угла A треугольника ABC, изображённого на рисунке.

Какое из следующих утверждений верно?

1) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.

2) Любая биссектриса равнобедренного треугольника является его медианой.

3) Сумма углов любого треугольника равна 360 градусам.

В ответе запишите номер выбранного утверждения.

Найдите значение выражения \(61a - 11b + 50\), если \(\dfrac{2a - 7b + 5}{7a - 2b + 5} = 9\).

Рыболов в 5 часов утра на моторной лодке отправился от пристали против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани (в км) он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч.

Найдите \(p\) и постройте график функции \(y=x^{2}+p\), если известно, что прямая \(y=-2x\) имеет с графиком равно одну общую точку.

Медианы тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Най­ди­те длину медианы, проведённой к сто­ро­не BC, если угол BAC равен 49°, угол BMCравен 131°, BC=4√3.

В параллелограмме ABCD точка K — середина стороны CD. Известно, что AK=BK. Докажите, что данный параллелограмм — прямоугольник.

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=48, BC=16, CF:DF=5:3.