Ежедневные тесты
Меню курса
Январь
Беседа ВК для обсуждения тестов: Вступить
Сложность теста - это диапазон сложности задач, которые в этот тест попали. Сложность задачи на сайте - это процент неверных ответов на неё. Уровень сложности "реального экзамена" примерно 0-40%. Более сложные задачи тоже из ФИПИ, но это редкость. 95+% задач сайта взяты из ФИПИ, сборников Ященко или полностью аналогичны им.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 32°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Даны векторы \(\vec{a}(0;3)\), \(\vec{b}(-2;4)\) и \(\vec{c}(4;-1)\). Найдите длину вектора \(\vec{a}+2\vec{b}+\vec{c}\)
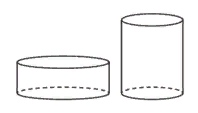
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго – 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Симметричную монету подбрасывают трижды. Найдите вероятность того, что "орел" выпадет ровно один раз.
В Волшебной стране бывает два типа погоды: хорошая и отличная. Причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 21 мая погода в Волшебной стране отличная. Найдите вероятность того, что 23 мая в Волшебной стране будет хорошая погода.
Решите уравнение \(\log_4(x+2)=\log_4(x^2+3x-13)\). Если корней несколько, в ответ запишите меньший из них.
Найдите значение выражения \(\dfrac{g(x+2)}{g(x)}\), если \(g(x)=15^x\).
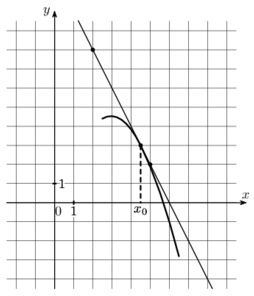
На рисунке изображены график функции \(y=f(x)\) и касательная к этому графику, проведенная в точке с абциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Автомобиль, движущийся в начальный момент времени со скоростью \(v_0 = 30\) м/с, начал торможение с постоянным ускорением \(a = 4\) м/с². За \(t\) секунд после начала торможения он прошел путь \(S = v_{0}t - \dfrac{at^2}{2} \) метров. Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.
Для организации пляжа на грузовике перевозится 611 тонн песка из карьера. В первый день грузовик перевез 5 тонн песка. Ежедневно увеличивая норму перевозки на одно и то же число тонн, грузовик перевез весь песок за 13 дней. Определите, сколько тонн песка было перевезено за девятый день.
На рисунке изображен график функции \(f(x)=k|x+a|+b\). Найдите \(f(-19)\).

Найдите точку минимума функции \(y =\sqrt{x^2 - 12x + 55}\).
а) Решите уравнение \(\dfrac{4}{\sin^2{\left(\frac{7\pi}{2}-x\right)}}-\dfrac{11}{\cos{x}}+6=0\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\frac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что M – середина SB.
б) Найдите расстояние между прямыми AC и DM, если высота пирамиды равна 6√3.
Решите неравенство \(\dfrac{\log_2(8x)\cdot \log_3(27x)}{x^2-|x|}⩽0\)
В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей.
На гипотенузе \(AB\) и катетах \(BC\) и \(AC\) прямоугольного треугольника \(ABC\) отмечены точки \(M\), \(N\) и \(K\) соответственно, причём прямая \(NK\) параллельна прямой \(AB\) и \(BM=BN=\dfrac{1}{2}KN\). Точка \(Р\) - середина отрезка \(KN\).
а) Докажите, что четырёхугольник \(BCPM\) - равнобедренная трапеция.
б) Найдите площадь треугольника \(ABC\), если \(BM=1\) и \(\angle BCM=15°\)
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}a(x^2+y^2)-ax+(a-3)y+1=0\\xy-1=y-x\end{cases}\) имеет ровно четыре различных решения.
В ящике лежит 58 овощей, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей, масса каждого из которых меньше 1000 г, равна 976 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1036 г.
а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г?
б) Могло ли в ящике оказаться ровно 12 овощей, масса каждого из которых равна 1000 г?
в) Какую наименьшую массу может иметь овощ в этом ящике?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.